Figure 3 from Application of M/G/1/K model for aggregated VoIP traffic packet loss estimation

M&G Monogram by MAYBE...

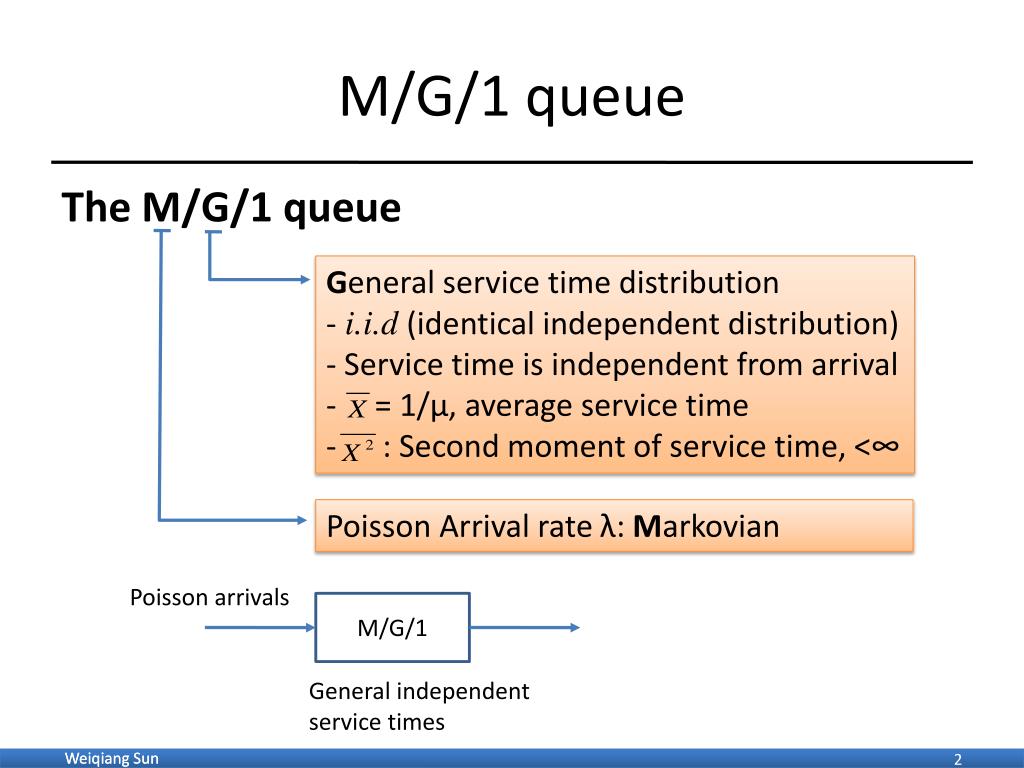
The M/G/1 Queue We discussed the M=G=1 queue; see Example 4.1 (A), p. 164, Example 4.3 (A), pp. 177-179, and Exercise 4.15 in Ross. See Examples 4.1 (B) and 4.3 (B) for a treatment of the G=M=1 queue. The M=G=1 queue has a Poisson arrival process (the M for Markov), IID service times with a general cdf G, one server and unlimited waiting space.

UT5LrJzZEHWTDZL819clRt1Bj5pvCUdHnsrCXWz0Gr6lZ5M420Afs2hxUzhZ1TpOcl_IqB6_zg=s900ckc0x00ffffff

The M/G/1 theory is a powerful tool, generalizing the solution of Markovian queues to the case of general service time distributions. There are many applications of the M/G/1 theory in the field of telecommunications; for instance, it can be used to study the queuing of fixed-size packets to be transmitted on a given link (i.e., M/D/1 case).

O.M.G YouTube

Madan, K.C.: An M/G/1 queue with second optional service. Queueing Syst. 34, 37-46 (2000) Article MathSciNet Google Scholar Gupur, G.: Analysis of the M/G/1 retrial queueing model with server breakdowns. J. Pseudo-Differ. Oper. Appl. 3, 313-340 (2010) Article MathSciNet Google Scholar

Histogram of 100M response times from the M/G/1 model. Download Scientific Diagram

The M/G/1 queueing system is one of the most fruitful models of Queueing Theory, and a huge literature concerning this model exists. The analytic techniques used for the investigation of this model are quite often too powerful and thus lead to rather intricate derivations of essentially simple results.

Figure 4 from An M/G/1 Model for Gigabit Energy Efficient Links With Coalescing and

The first crash, in October 2018, involved a 737 Max 8 operated by Indonesia's Lion Air that killed 189. The second incident was in March 2019, when an Ethiopian Airlines flight, also a 737 Max 8.

Dhanush M G Production Engineer Rakshu Engineering LinkedIn

Basic Model Arrivals Departures Queue Server CS 756 2 Major parameters: interarrival-time distribution service-time distribution number of servers queueing discipline (how customers are taken from the queue, for example, FCFS) number of buffers, which customers use to wait for service

Figure 4 from The M/G/1 fluid model with heavytailed message length distributions Semantic

Model definition [ edit] A queue represented by a M/G/1 queue is a stochastic process whose state space is the set {0,1,2,3.}, where the value corresponds to the number of customers in the queue, including any being served.

PPT M/G/1 queue PowerPoint Presentation, free download ID2052454

Daniel Myers This lectures deals with some variations to the basic M/G/1 model, and their applications to real systems. Approximating a G/G/1 Queue The G/G/1 queue has both general service times and a general arrival process.

PPT Modelo m/G/1 PowerPoint Presentation, free download ID6494904

In queueing theory, a discipline within the mathematical theory of probability, an M/M/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times have an exponential distribution. The model name is written in Kendall's notation.

MG 1

The M/G/1 queue In many applications, the assumption of exponentially distributed service times is not realistic (e.g., in production systems). Therefore, we will now look at a model with generally distributed service times. Model: Arrival process is a Poisson process with rate λ.

Figure 3 from Application of M/G/1/K model for aggregated VoIP traffic packet loss estimation

M/G/1 Queueing Model Basic Concepts The M/G/1 queueing model is similar to the M/M/1 model except that the service rate follows a general distribution. This means that the service rate distribution can be any distribution with mean μ and standard deviation σ.

m/g/1 model YouTube

• For analyzing the G/M/1 queue using the Imbedded Markov Chain approach, the imbedded points are chosen to be the arrival instants of jobs to the system • System State = Number in the system immediately before an arrival instant ni= Number in the system just before the itharrival si+1 = Number of jobs served between the iththand the (i+1).

AGIKgqNhT4_y_qwtmyxWco5f13M8y1mA7aMl7r4WnladMg=s900ckc0x00ffffffnorj

Also, to increase the flexibility of using the M/G/1 model with cyclic service times in optimization problems, an approximation approach is introduced in order to obtain the average number of customers in the system. Finally, using this approximation, the optimal N-limited service policy for a single vacation queueing system is obtained.

M G 1 AMA Academy of Model Aeronautics

Our analyses for M/M/1 and M/G/1 queuing models will depend heavily on probability. To that extent, we dedicate this section towards reviewing concepts regarding Poisson point processes and continuous-time markov chains. The content from this section is an adaptation of that presented here1. The reader may refer to this as a secondary source.

(PDF) An analysis of the M/G/1 system with N and T policy Sun Hur Academia.edu

Summary. We study a queueing system with memoryless Poisson arrivals and generally distributed processing times, the so-called M/G/1 system. Performance measures of this system can be derived exactly, using the principle of work conservation and the property of PASTA (Poisson arrivals see time averages).

Figure 4 from M/G/1/K SYSTEM WITH PUSHOUT SCHEME UNDER VACATION POLICY Semantic Scholar

In queueing theory, a discipline within the mathematical theory of probability, an M/G/k queue is a queue model where arrivals are M arkovian (modulated by a Poisson process ), service times have a G eneral distribution and there are k servers.