(PDF) Upper Bound Estimation of Logarithmic Derivative Norm of

LOne Norm of Derivative Objective
This norm can be defined as the square root of the inner product of a vector with itself. A seminorm satisfies the first two properties of a norm, but may be zero for vectors other than the origin. [1] A vector space with a specified norm is called a normed vector space.

Derivative of the 2norm of a multivariate function YouTube
derivatives - Differentiation of vector norms - Mathematics Stack Exchange Differentiation of vector norms Asked 10 years, 11 months ago Modified 7 years, 9 months ago Viewed 50k times 15 I want to solve the following equation ∂ ∂β[||y −Xβ||2 +||β||2] = 0 ∂ ∂ β [ | | y − X β | | 2 + | | β | | 2] = 0 for β β.

(PDF) Upper Bound Estimation of Logarithmic Derivative Norm of
1 How should I differentiate the norm of a function? I mean, how can I get the first and second derivatives of something like: ||α(s)||2 I know that I have to use the chain rule, but I am struggling with it. Thanks. derivatives normed-spaces chain-rule Share Cite Follow edited Sep 13, 2019 at 3:49 dmtri 3,256 3 15 29 asked Sep 13, 2019 at 2:50
Derivative of norm of function w.r.t realpart of function
Subject classifications. Let X and Y be Banach spaces and let f:X->Y be a function between them. f is said to be Gâteaux differentiable if there exists an operator T_x:X->Y such that, for all v in X, lim_ (t->0) (f (x+tv)-f (x))/t=T_xv. (1) The operator T_x is called the Gâteaux derivative of f at x. T_x is sometimes assumed to be bounded.
Derivative of norm of function w.r.t realpart of function
The concept of logarithmic derivative μ [ A] is used in [2], [1] in the theory of ordinary differential equations to obtain new results, e.g., in stability problems, and the results improve those obtained by using the norm ∥ A ∥.

linear algebra 2norm of a diagonal matrix and its relation to
The norm is extensively used, for instance, to evaluate the goodness of a model. By the end of this tutorial, you will hopefully have a better intuition of this concept and why it is so valuable in machine learning. We will also see how the derivative of the norm is used to train a machine learning algorithm.

linear algebra For vector pnorm, can we prove it is decreasing
However, it is far easier to differentiate this function by first rewriting it as f(x) = 6x − 2. f′ (x) = d dx( 6 x2) = d dx(6x − 2) Rewrite 6 x2 as 6x − 2. = 6 d dx(x − 2) Apply the constant multiple rule. = 6( − 2x − 3) Use the extended power rule to differentiate x − 2. = − 12x − 3 Simplify. Exercise 3.3.8.
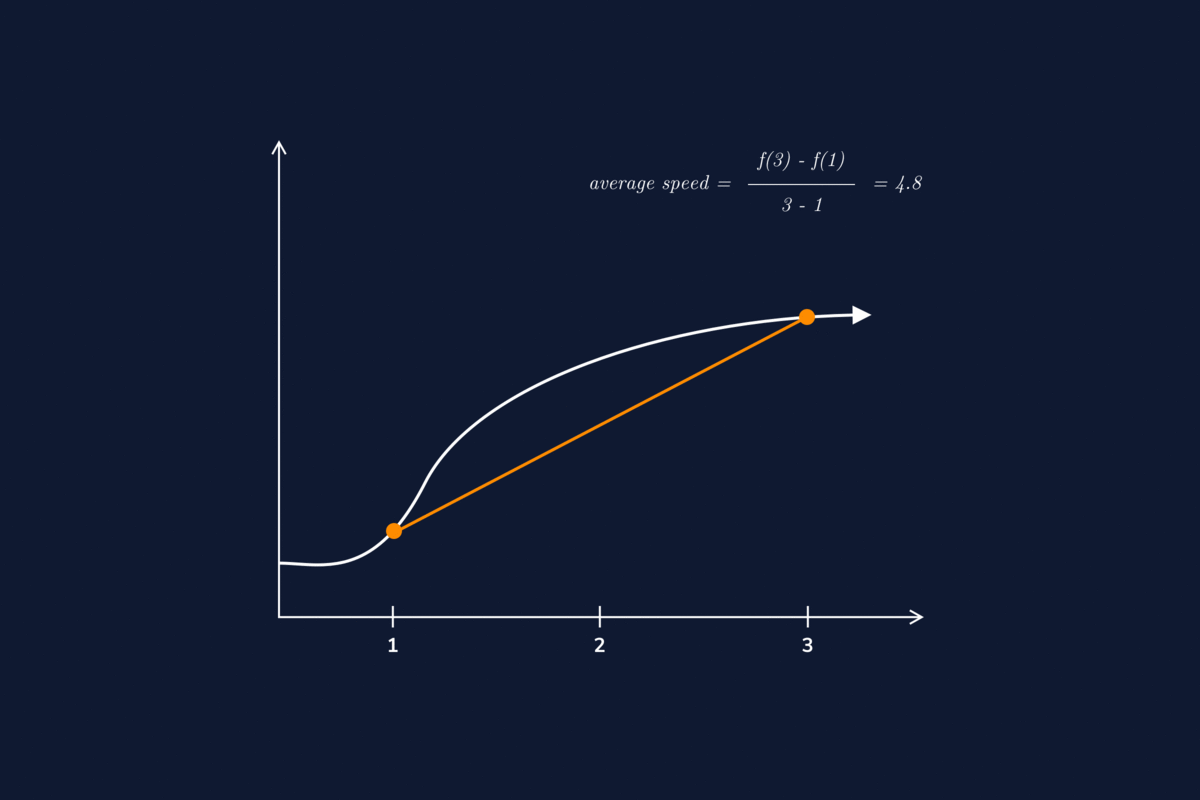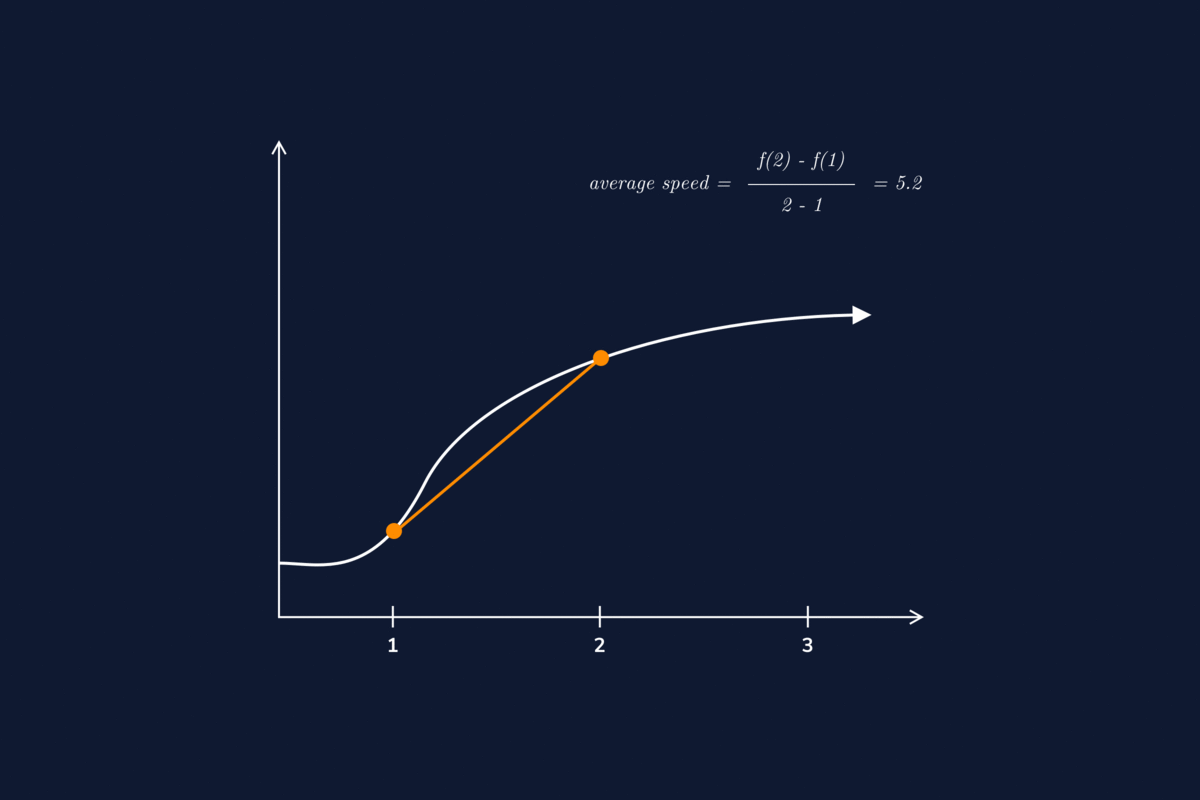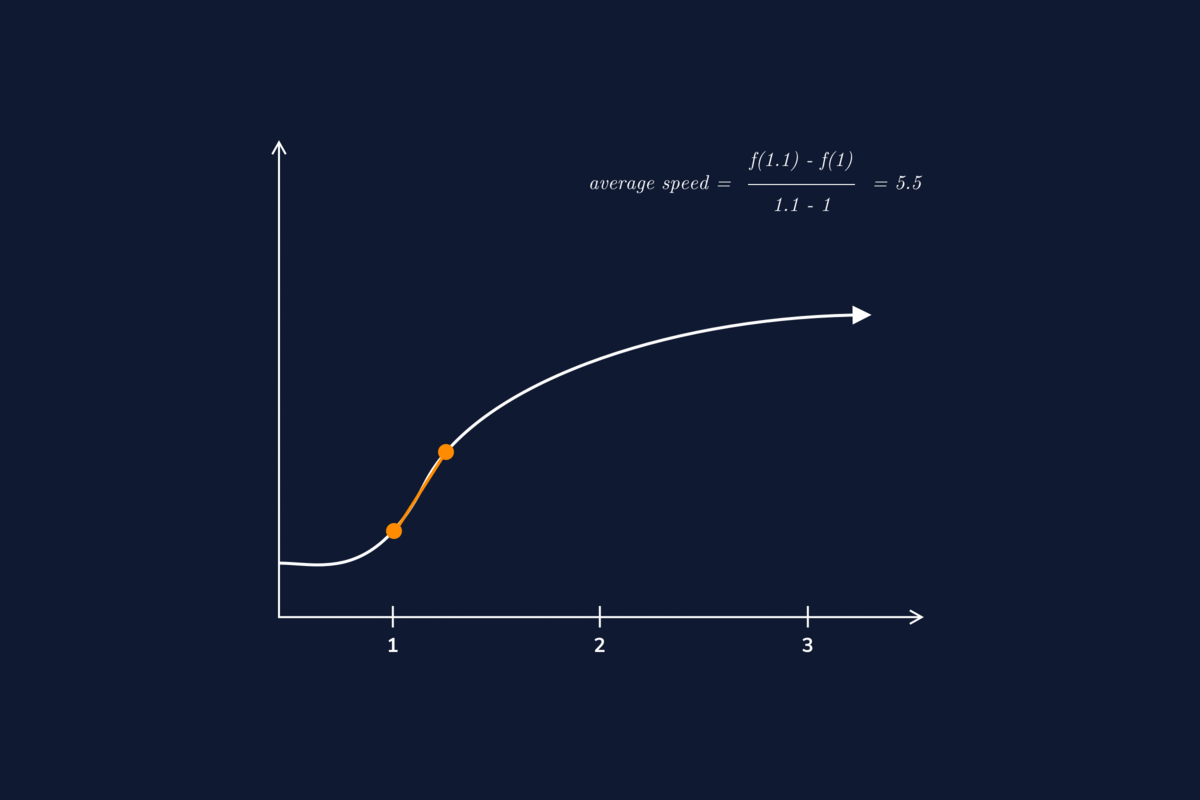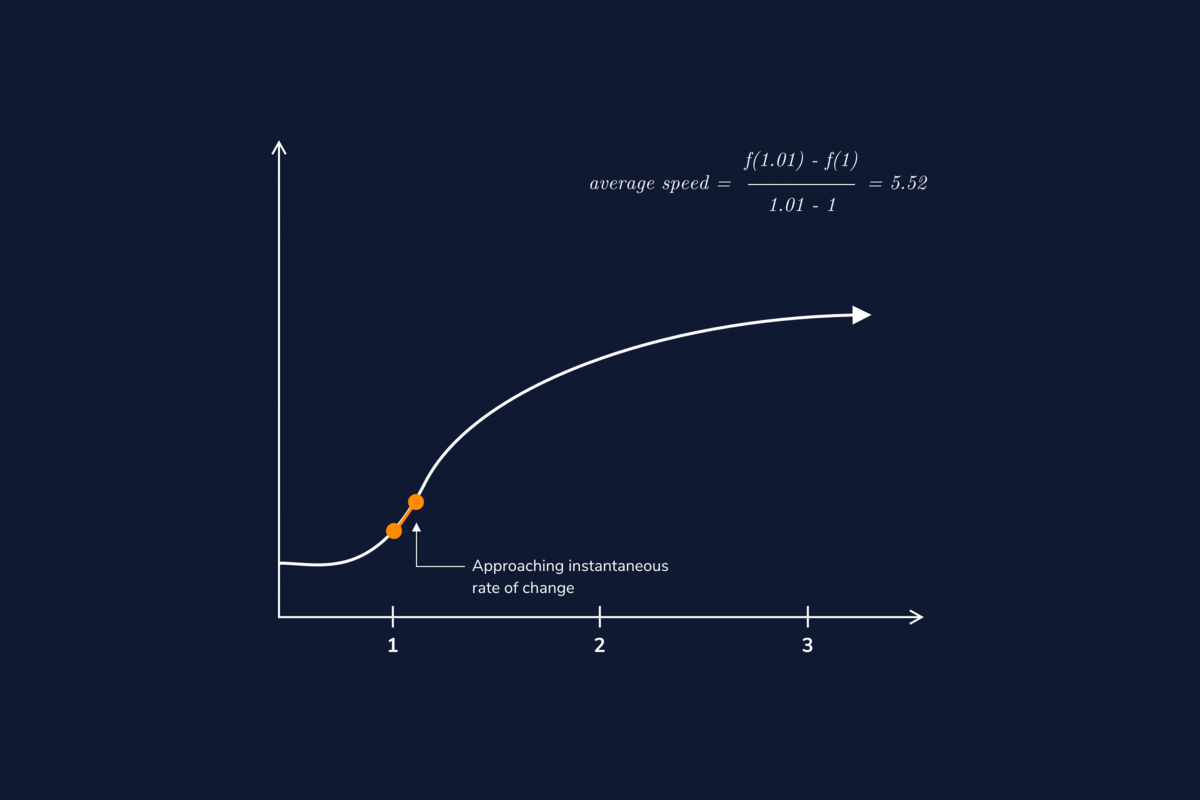
Differential Calculus Differential Calculus Cheatsheet Codecademy
The Gateaux derivative of k · k at vin direction of uis defined as lim t→0 kv+tuk −kvk t. We say k · k is Gateaux differentiable at 0 6= vif and only if for all u∈ V, lim t→0 kv+tuk−kvk t exists. A concept related to the Gateaux derivative of norm function is the subdifferential set of norm function (see [9]). The subdifferential set

linear algebra Derivatives Across Summations Mathematics Stack Exchange
Differential Integral Series Vector Multivariable Advanced Specialized Miscellaneous v t e The derivative is a fundamental tool of calculus that quantifies the sensitivity of change of a function 's output with respect to its input.

Derivative by First Principle Brilliant Math & Science Wiki
We find an expression for Gateaux derivative of the C∗ -algebra norm. This gives us alternative proofs or generalizations of various known results on the closely related notions of subdifferential sets, smooth points and Birkhoff-James orthogonality for spaces B(H) and Cb(Ω). We also obtain an expression for subdifferential sets of the norm.
[Solved] Derivative of the squared L^2 norm of a 9to5Science
Definition 4.3. A matrix norm ��on the space of square n×n matrices in M n(K), with K = R or K = C, is a norm on the vector space M n(K)withtheadditional property that �AB�≤�A��B�, for all A,B ∈ M n(K). Since I2 = I,from�I� = � �I2 � � ≤�I�2,weget�I�≥1, for every matrix norm.

Solved Find the derivative R'(t) and norm of the derivative.
Symbolab is the best derivative calculator, solving first derivatives, second derivatives, higher order derivatives, derivative at a point, partial derivatives, implicit derivatives, derivatives using definition, and more. Is velocity the first or second derivative? Velocity is the first derivative of the position function.

Where's my mistake? Manual Derivative of Layer Norm seems to not allow
The derivative of a vector-valued function can be understood to be an instantaneous rate of change as well; for example, when the function represents the position of an object at a given point in time, the derivative represents its velocity at that same point in time. We now demonstrate taking the derivative of a vector-valued function.

Solved (1 point) Given Find the derivative R'(t) and norm of
This notion of derivative is a generalization of the ordinary derivative of a function on the real numbers since the linear maps from to are just multiplication by a real number. In this case, is the function Properties A function differentiable at a point is continuous at that point.
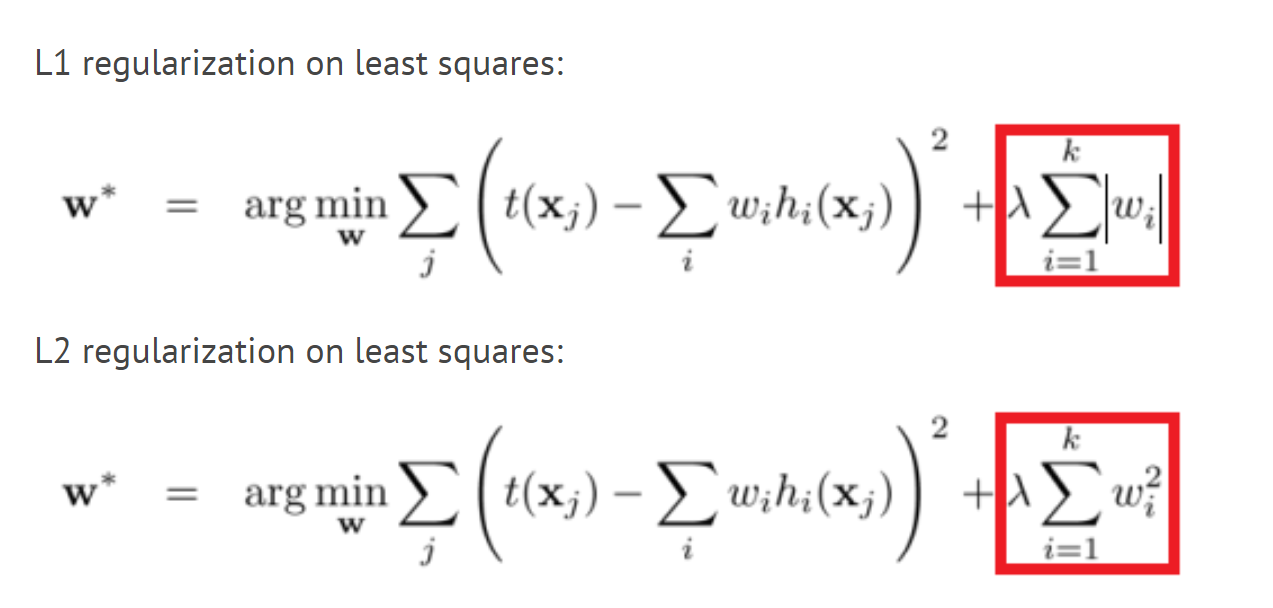
Only Numpy Implementing Different combination of L1 /L2 norm
One way to approach this to define x = Array [a, 3]; Then you can take the derivative x = D [x . x, {x}] and you'll get more what you expect. Otherwise it doesn't know what the dimensions of x are (if its a scalar, vector, matrix). - bill s. Apr 11, 2021 at 20:17. Thanks, now it makes sense why, since it might be a matrix.

calculus The derivative of a moving L2 norm Mathematics Stack Exchange
Derivative of the 2 -norm of a multivariate function Ask Question Asked 10 years, 11 months ago Modified 3 months ago Viewed 92k times 33 I've got a function g(x, y) = ‖f(x, y)‖2 and I want to calculate its derivatives with respect to x and y. Using Mathematica, differentiating w.r.t. x gives me f ′ x(x, y)Norm ′ (f(x, y)), where Norm is ‖ ⋅ ‖.