How To Find The Derivative Of A Fraction With A Square Root In The

Here we use the known power rule for y = x2 y = x 2 to find the derivative of its inverse function, y = x−−√ = x1/2 y = x = x 1 / 2. This general idea recurs in later chapters when we introduce new functions and their inverses. Example 9.7: Derivative of x−−√ x. Consider the function y = x−−√ = x1/2 y = x = x 1 / 2.

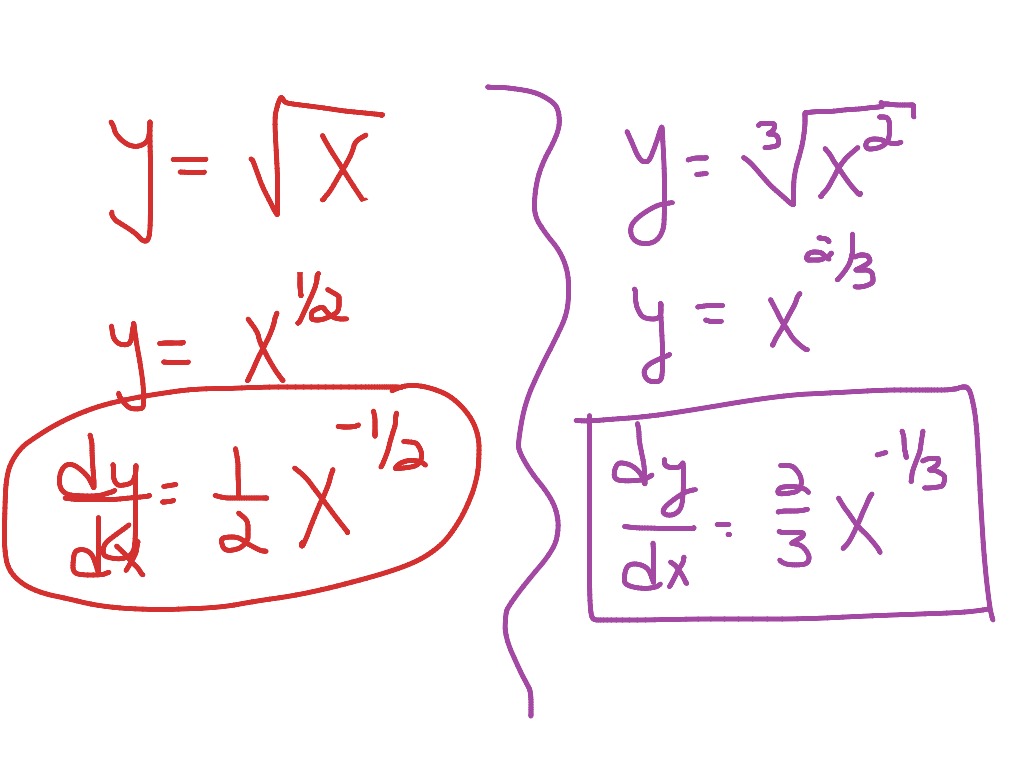
Derivatives Power rule with fractional exponents Math ShowMe

This calculus video tutorial provides a basic introduction into the quotient rule for derivatives. It explains how to find the derivatives of fractions and.

Second Derivative with Fraction Example YouTube

The derivative of a function describes the function's instantaneous rate of change at a certain point. Another common interpretation is that the derivative gives us the slope of the line tangent to the function's graph at that point. Learn how we define the derivative using limits.

Example 19 Find derivative from first principle f(x) = (2x + 3)/(x

This calculus video tutorial explains how to find the derivative of rational functions. It explains how to use the power rule, chain rule, and quotient rule.

How To Find The Derivative Of A Fraction With A Square Root In The

The derivative f ′ (a) at a specific point x = a, being the slope of the tangent line to the curve at x = a, and. The derivative as a function, f ′ (x) as defined in Definition 2.2.6. Of course, if we have f ′ (x) then we can always recover the derivative at a specific point by substituting x = a.

How To Find The Second Derivative Of A Fraction

The quotient rule states that to find the derivative of a fraction, you differentiate the numerator and denominator separately, and then divide the difference of the two derivatives by the square of the denominator. This can be represented as (d/dx) (u/v) = (v * du/dx - u * dv/dx) / v^2, where u and v represent functions of x..

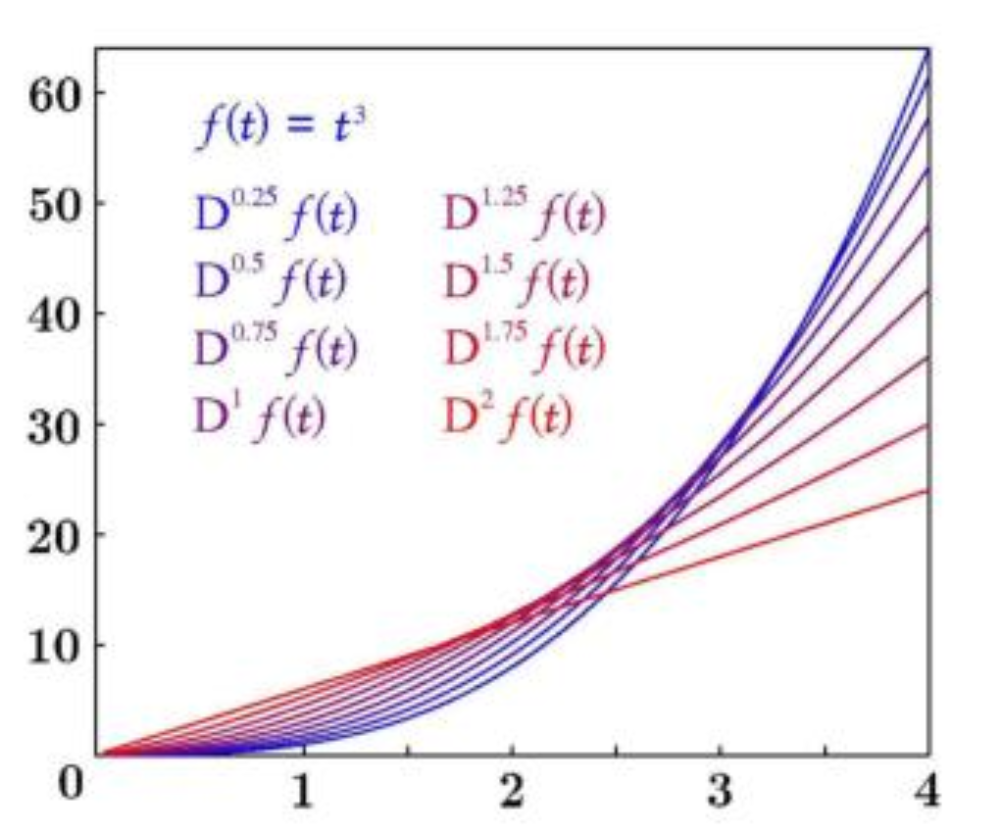
Efficient evaluation of fractional derivatives Institut für

In this chapter we introduce Derivatives. We cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well as derivatives of polynomials, roots, trig functions, inverse trig functions, hyperbolic functions, exponential functions and logarithm functions. We also cover implicit differentiation, related rates, higher order derivatives and logarithmic.

Derivatives of Rational Functions YouTube

Explanation: When we are given a fraction say f (x) = 3 −2x − x2 x2 − 1. This comprises of two fractions - say one g(x) = 3 −2x − x2 in numerator and the other h(x) = x2 − 1, in the denominator. Here we use quotient rule as described below. Quotient rule states if f (x) = g(x) h(x) then df dx = dg dx × h(x) − dh dx ×g(x) (h(x))2

How To Find The Derivative of a Fraction Calculus YouTube

Definitions Derivative ( generalizations) Differential infinitesimal of a function total Concepts Differentiation notation Second derivative Implicit differentiation Logarithmic differentiation Related rates Taylor's theorem Rules and identities Sum Product Chain Power Quotient L'Hôpital's rule Inverse General Leibniz Faà di Bruno's formula

Find Derivative Of Polynomial Fraction With Quotient Rule f(x) = (x^5

In applied mathematics and mathematical analysis, a fractional derivative is a derivative of any arbitrary order, real or complex. Its first appearance is in a letter written to Guillaume de l'Hôpital by Gottfried Wilhelm Leibniz in 1695. [2]

Constant Multiple Rule for Derivatives (With Proof and Examples

Courses on Khan Academy are always 100% free. Start practicing—and saving your progress—now: https://www.khanacademy.org/math/old-ap-calculus-ab/ab-derivati.

The Derivative of a Constant (With Examples) Owlcation

The Derivative tells us the slope of a function at any point. There are rules we can follow to find many derivatives. For example: The slope of a constant value (like 3) is always 0 The slope of a line like 2x is 2, or 3x is 3 etc and so on. Here are useful rules to help you work out the derivatives of many functions (with examples below ).

How To Find The Derivative Of A Fraction With A Square Root In The

Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more.. A rational function can be split into partial fractions before taking the derivative, but this is often a more lengthy process than just doing the quotient rule. Comment Button navigates to signup page (1 vote)

Differentiation of fractions YouTube

Defintion of the Derivative The derivative of f (x) f ( x) with respect to x is the function f ′(x) f ′ ( x) and is defined as, f ′(x) = lim h→0 f (x+h) −f (x) h (2) (2) f ′ ( x) = lim h → 0 f ( x + h) − f ( x) h Note that we replaced all the a 's in (1) (1) with x 's to acknowledge the fact that the derivative is really a function as well.

Example Derivatives With Fractions YouTube

This calculus video explains how to find the derivative of a fraction using the power rule and quotient rule. Examples include square roots in fractions.De.

How To Find The Derivative Of A Fractional Exponent

Symbolab is the best derivative calculator, solving first derivatives, second derivatives, higher order derivatives, derivative at a point, partial derivatives, implicit derivatives, derivatives using definition, and more. Is velocity the first or second derivative? Velocity is the first derivative of the position function.